



Next: Calculated Line Intensities
Up: Estimates of Line
Previous: Spectral line intensities
The total intensities of the Ly- and O VI lines reported in this
chapter have been calculated for different configurations of coronal holes
and for the quiet unstructured corona, using the plasma parameters obtained
by two types of solar wind model, a two--fluid model developed by Esser et
al. (1986) and a one--fluid radiative energy balance model developed by
Withbroe (1988). Here we describe the principal characteristics of these
models.
and O VI lines reported in this
chapter have been calculated for different configurations of coronal holes
and for the quiet unstructured corona, using the plasma parameters obtained
by two types of solar wind model, a two--fluid model developed by Esser et
al. (1986) and a one--fluid radiative energy balance model developed by
Withbroe (1988). Here we describe the principal characteristics of these
models.
The plasma parameters chosen at the coronal base for Esser et al. (1986)
model are given in Table 2 for each region, while the density velocity and
temperature profiles are shown in Figures 3.1 and 3.2. The density profile for
the coronal hole (Figure 3.1a, solid line) is compared to the lowest density
profile derived by Lallement et al.(1986) for the coronal hole described
by Munro and Jackson (1977). These are the lowest coronal hole densities
that we could find in the literature, and the hole must therefore be
considered rather extreme. The corresponding velocities (dashed line in
Figure 3.1a) are compared to velocities derived from Doppler dimming by
Strachan (1990) (triangles), and velocities derived from Interplanetary
Scintillation measurements by Tyler et al. (1981) (square), and from
measurements of Doppler shifts in Mg X 625 by Rottman et al. (1982)
(circle). Note that there are even fewer velocity measurements in the
inner corona than density measurements.
In section 3.2.3 we have calculated the line intensities for two cases, one with
the velocity shown in Figure 3.1a, and one with a velocity that is approximately
constant below 3.5 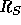 . Electron and proton thermal
temperatures are shown in Figure 3.1b (solid line and dashed line respectively),
as none of these temperatures have been measured before there is not much
to compare them with. The
proton thermal temperature in Figure 3.1b falls off slightly slower than adiabatically
due to the
coupling to the electrons, the electron temperature is assumed to
be given by:
. Electron and proton thermal
temperatures are shown in Figure 3.1b (solid line and dashed line respectively),
as none of these temperatures have been measured before there is not much
to compare them with. The
proton thermal temperature in Figure 3.1b falls off slightly slower than adiabatically
due to the
coupling to the electrons, the electron temperature is assumed to
be given by:

This is the expression for a conductively dominated electron gas where
the conduction is given by the Spitzer (1962) formula (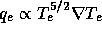 ), and the temperature vanishes at
), and the temperature vanishes at
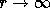 . The electron and proton thermal temperatures at the coronal
base are set equal
. The electron and proton thermal temperatures at the coronal
base are set equal 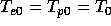 .
This electron temperature profile is only an estimate.
The values at the coronal base (Table 2) are inside
observed limits. The effective temperature, which is also shown in Figure
3.1b (dotted line), is given by:
.
This electron temperature profile is only an estimate.
The values at the coronal base (Table 2) are inside
observed limits. The effective temperature, which is also shown in Figure
3.1b (dotted line), is given by:
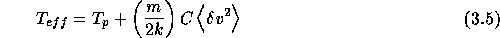
where C is a constant which was chosen to be 1 (e.g., Esser et al. 1986;
Maltby 1968), and 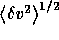 is the
Alfvén wave velocity amplitude, k the Boltzman constant, m the mass
of the scattering particles. This expression applies only if the line profile
is Gaussian, and the only source of non-thermal broadening is due to
Alfvén waves (see also Esser, 1990, and references therein.
is the
Alfvén wave velocity amplitude, k the Boltzman constant, m the mass
of the scattering particles. This expression applies only if the line profile
is Gaussian, and the only source of non-thermal broadening is due to
Alfvén waves (see also Esser, 1990, and references therein.
The Alfvén wave velocity amplitude is calculated from the expression
(Hollweg 1973; Jacques 1977)
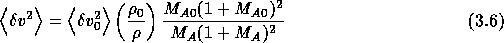
3.1 Esser et al. (1986) model. 3.2 Withbroe (1988) model.
Figure 3.1. Assumed plasma parameters for the coronal hole,
(a) outflow velocity solid line, and density (dashed line). (b)
electron, proton and effective proton temperature (solid line,
dashed line and dotted line respectively). Symbols refer to observed
quantities (see text for details).
Figure 3.2. Assumed plasma parameters for the low speed solar wind.
Symbols as in Figure 3.1.
Here 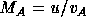 is the Alfvén Mach number,
is the Alfvén Mach number, 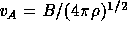 ,
is the Alfvén speed,
,
is the Alfvén speed, 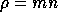 the mass density, u the flow speed, and
n the electron density (
the mass density, u the flow speed, and
n the electron density (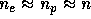 ), both are taken from
Figure 3.1a.
), both are taken from
Figure 3.1a.
The calculated effective temperature is compared in Figure 3.1b to temperatures
derived from Lyman- line width observations (dots) by Withbroe et al.
(1985 and 1986). The assumed wave velocity amplitude at the coronal base,
and magnetic field strength are also inside observational limits
(e.g., Hollweg et al. 1982).
The magnetic field strength given in Table 2 has to be multiplied by the
expansion factor of the coronal hole which was taken to be 7.26 (e.g., Munro
and Jackson 1977).
line width observations (dots) by Withbroe et al.
(1985 and 1986). The assumed wave velocity amplitude at the coronal base,
and magnetic field strength are also inside observational limits
(e.g., Hollweg et al. 1982).
The magnetic field strength given in Table 2 has to be multiplied by the
expansion factor of the coronal hole which was taken to be 7.26 (e.g., Munro
and Jackson 1977).
The calculated velocity at 1 AU for the region considered in Figure 3.1 is about
1370 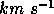 and the mass flux approximately
and the mass flux approximately
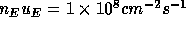 . This is the lowest mass flux value
given by Withbroe (1988).
. This is the lowest mass flux value
given by Withbroe (1988).
The density as a function of heliocentric distance in the quiet
unstructured corona is plotted in Figure 3.2a (solid line), and compared
to densities derived from polarization brightness observations by Saito (1970,
dots) for the equatorial direction, and by Allen (1973, crosses) for solar
maximum. For the outflow velocity of this region (dashed line in Figure 3.2a)
we have only an upper observational limit derived by Withbroe et al. (1982a)
from Ly- Doppler dimming. In Figure 3.2b we have plotted the proton,
electron and effective temperatures. The proton temperature again falls off
less steeply than adiabatically, the electron temperature is given by
Equation (4), and the effective temperature by Equation (5). For comparison
we have also plotted the temperatures derived from EUV intensity measurements
and Ly-
Doppler dimming. In Figure 3.2b we have plotted the proton,
electron and effective temperatures. The proton temperature again falls off
less steeply than adiabatically, the electron temperature is given by
Equation (4), and the effective temperature by Equation (5). For comparison
we have also plotted the temperatures derived from EUV intensity measurements
and Ly- line width measurements (see Withbroe 1988, and references
therein) and, at 3
line width measurements (see Withbroe 1988, and references
therein) and, at 3
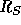 , a temperature derived from charge state measurements (Bame et al. 1974).
It is not known whether the temperatures determined from the optical
measurements correspond to a magnetically open or closed region. Comparing
to other temperature measurements it seems more likely that this was a closed
region, and we have therefore chosen temperatures that are significantly lower
for the intensity calculations. Note that this increases the ion equilibrium
values of the O VI ions.
, a temperature derived from charge state measurements (Bame et al. 1974).
It is not known whether the temperatures determined from the optical
measurements correspond to a magnetically open or closed region. Comparing
to other temperature measurements it seems more likely that this was a closed
region, and we have therefore chosen temperatures that are significantly lower
for the intensity calculations. Note that this increases the ion equilibrium
values of the O VI ions.
TABLE 2. Parameter Values for Esser et al. (1986) Model
(Calculated line intensities in 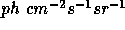 ).
).
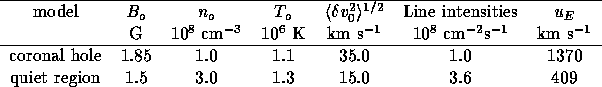
Spadaro and Ventura (1993), by adopting a one--fluid radiative energy
balance model developed by Withbroe (1988), calculated the intensities of
the O VI 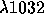 and
and 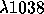 lines expected from an equatorial
and a polar coronal hole at solar minimum, when observed on the plane of
the sky in the 1.2
lines expected from an equatorial
and a polar coronal hole at solar minimum, when observed on the plane of
the sky in the 1.2 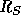 -- 8
-- 8 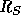 range of heliocentric
distance. They also considered the contribution from the quiet unstructured
corona surrounding tha coronal holes. The Withbroe (1988) model describes the
coronal holes as radial flow tubes with a cross--sectional area which has a
non--radial increase with the heliocentric distance. The non--radial
expansion factor is given by Kopp and Holzer (1976).
range of heliocentric
distance. They also considered the contribution from the quiet unstructured
corona surrounding tha coronal holes. The Withbroe (1988) model describes the
coronal holes as radial flow tubes with a cross--sectional area which has a
non--radial increase with the heliocentric distance. The non--radial
expansion factor is given by Kopp and Holzer (1976).
The radial profiles of the coronal electron densities, temperatures and
outflow speeds inside the structures considered are plotted in Figure 3.3 (see
Withbroe 1988, for a comparison of these profiles with observations). The
boundaries of the two coronal holes are shown in Figure 3.4. Note that the
polar hole is much broader than the equatorial hole and is similar to the
coronal hole described by Munro and Jackson (1977).
Figure 3.3. Densities (top), temperatures (centre) and flow
velocities (bottom) of the considered coronal models. Solid curves are
relative to the equatorial hole at the solar minimum, dot curves to the
polar coronal hole at the solar minimum, and dashed curves to the quiet
unstructured corona (from Withbroe 1988).
Figure 3.4. Geometry of the simulated observations of the two
coronal holes surrounded by the quiet corona (from Spadaro and Ventura
1993).
The O VI kinetic temperature and outflow velocity have been assumed to be
equal to the corresponding plasma values. The atomic parameters are those
reported in Table 1, as well as the intensity and profile of the
chromospheric exciting lines. The effect of non--thermal motions, such as
the Alfvén waves, on the simulated line profiles (e.g, Esser 1990) has
not been considered.
The contribution from the quiet corona has also been calculated by
arbitrarily setting the outflow velocity equal to zero and leaving the
other physical parameters unchanged, in order to consider tha case of the
coronal hole surrounded by a static atmosphere, such as that confined in
magnetic closed regions. This is only a rough estimate of the contribution
from the static quiet corona. A better evaluation requires more detailed
models.




Next: Calculated Line Intensities
Up: Estimates of Line
Previous: Spectral line intensities
Peter Smith
Fri Jan 17 12:11:15 EST 1997
 and O VI lines reported in this
chapter have been calculated for different configurations of coronal holes
and for the quiet unstructured corona, using the plasma parameters obtained
by two types of solar wind model, a two--fluid model developed by Esser et
al. (1986) and a one--fluid radiative energy balance model developed by
Withbroe (1988). Here we describe the principal characteristics of these
models.
and O VI lines reported in this
chapter have been calculated for different configurations of coronal holes
and for the quiet unstructured corona, using the plasma parameters obtained
by two types of solar wind model, a two--fluid model developed by Esser et
al. (1986) and a one--fluid radiative energy balance model developed by
Withbroe (1988). Here we describe the principal characteristics of these
models.




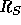 . Electron and proton thermal
temperatures are shown in Figure 3.1b (solid line and dashed line respectively),
as none of these temperatures have been measured before there is not much
to compare them with. The
proton thermal temperature in Figure 3.1b falls off slightly slower than adiabatically
due to the
coupling to the electrons, the electron temperature is assumed to
be given by:
. Electron and proton thermal
temperatures are shown in Figure 3.1b (solid line and dashed line respectively),
as none of these temperatures have been measured before there is not much
to compare them with. The
proton thermal temperature in Figure 3.1b falls off slightly slower than adiabatically
due to the
coupling to the electrons, the electron temperature is assumed to
be given by:

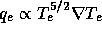 ), and the temperature vanishes at
), and the temperature vanishes at
 . The electron and proton thermal temperatures at the coronal
base are set equal
. The electron and proton thermal temperatures at the coronal
base are set equal  .
This electron temperature profile is only an estimate.
The values at the coronal base (Table 2) are inside
observed limits. The effective temperature, which is also shown in Figure
3.1b (dotted line), is given by:
.
This electron temperature profile is only an estimate.
The values at the coronal base (Table 2) are inside
observed limits. The effective temperature, which is also shown in Figure
3.1b (dotted line), is given by:
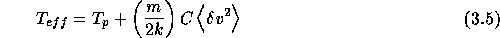
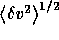 is the
Alfvén wave velocity amplitude, k the Boltzman constant, m the mass
of the scattering particles. This expression applies only if the line profile
is Gaussian, and the only source of non-thermal broadening is due to
Alfvén waves (see also Esser, 1990, and references therein.
is the
Alfvén wave velocity amplitude, k the Boltzman constant, m the mass
of the scattering particles. This expression applies only if the line profile
is Gaussian, and the only source of non-thermal broadening is due to
Alfvén waves (see also Esser, 1990, and references therein.
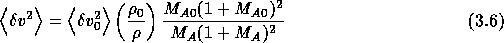
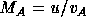 is the Alfvén Mach number,
is the Alfvén Mach number, 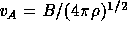 ,
is the Alfvén speed,
,
is the Alfvén speed, 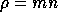 the mass density, u the flow speed, and
n the electron density (
the mass density, u the flow speed, and
n the electron density (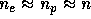 ), both are taken from
Figure 3.1a.
), both are taken from
Figure 3.1a.
 line width observations (dots) by Withbroe et al.
(1985 and 1986). The assumed wave velocity amplitude at the coronal base,
and magnetic field strength are also inside observational limits
(e.g., Hollweg et al. 1982).
The magnetic field strength given in Table 2 has to be multiplied by the
expansion factor of the coronal hole which was taken to be 7.26 (e.g., Munro
and Jackson 1977).
line width observations (dots) by Withbroe et al.
(1985 and 1986). The assumed wave velocity amplitude at the coronal base,
and magnetic field strength are also inside observational limits
(e.g., Hollweg et al. 1982).
The magnetic field strength given in Table 2 has to be multiplied by the
expansion factor of the coronal hole which was taken to be 7.26 (e.g., Munro
and Jackson 1977).
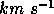 and the mass flux approximately
and the mass flux approximately
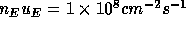 . This is the lowest mass flux value
given by Withbroe (1988).
. This is the lowest mass flux value
given by Withbroe (1988).
 Doppler dimming. In Figure 3.2b we have plotted the proton,
electron and effective temperatures. The proton temperature again falls off
less steeply than adiabatically, the electron temperature is given by
Equation (4), and the effective temperature by Equation (5). For comparison
we have also plotted the temperatures derived from EUV intensity measurements
and Ly-
Doppler dimming. In Figure 3.2b we have plotted the proton,
electron and effective temperatures. The proton temperature again falls off
less steeply than adiabatically, the electron temperature is given by
Equation (4), and the effective temperature by Equation (5). For comparison
we have also plotted the temperatures derived from EUV intensity measurements
and Ly- line width measurements (see Withbroe 1988, and references
therein) and, at 3
line width measurements (see Withbroe 1988, and references
therein) and, at 3
 , a temperature derived from charge state measurements (Bame et al. 1974).
It is not known whether the temperatures determined from the optical
measurements correspond to a magnetically open or closed region. Comparing
to other temperature measurements it seems more likely that this was a closed
region, and we have therefore chosen temperatures that are significantly lower
for the intensity calculations. Note that this increases the ion equilibrium
values of the O VI ions.
, a temperature derived from charge state measurements (Bame et al. 1974).
It is not known whether the temperatures determined from the optical
measurements correspond to a magnetically open or closed region. Comparing
to other temperature measurements it seems more likely that this was a closed
region, and we have therefore chosen temperatures that are significantly lower
for the intensity calculations. Note that this increases the ion equilibrium
values of the O VI ions.
 ).
).
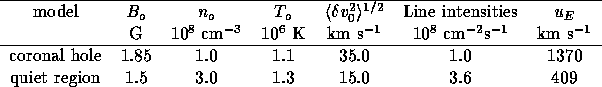
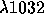 and
and 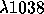 lines expected from an equatorial
and a polar coronal hole at solar minimum, when observed on the plane of
the sky in the 1.2
lines expected from an equatorial
and a polar coronal hole at solar minimum, when observed on the plane of
the sky in the 1.2 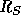 -- 8
-- 8 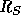 range of heliocentric
distance. They also considered the contribution from the quiet unstructured
corona surrounding tha coronal holes. The Withbroe (1988) model describes the
coronal holes as radial flow tubes with a cross--sectional area which has a
non--radial increase with the heliocentric distance. The non--radial
expansion factor is given by Kopp and Holzer (1976).
range of heliocentric
distance. They also considered the contribution from the quiet unstructured
corona surrounding tha coronal holes. The Withbroe (1988) model describes the
coronal holes as radial flow tubes with a cross--sectional area which has a
non--radial increase with the heliocentric distance. The non--radial
expansion factor is given by Kopp and Holzer (1976).