Articles:
1) ``Evidence for Magnetic and Virial Equilibrium in Molecular
Clouds.'' Myers, P. C.; Goodman, A. A. (ADS)Paper
I.
2) ``Magnetic Molecular Clouds: Indirect Evidence for Magnetic
Support and Ambipolar Diffusion.'' Myers, P. C.; Goodman, A.
A. (ADS)
Paper II
The observations were trends first observed by Larson
(1981) and subsequently by others which seem valid over a large
range of size and density scales in molecular clouds:
1) \sigma \propto R^{0.5}
2) n \propto R^{-1}
3) \sigma^{2} \simeq GM/R
where `\sigma' is the velocity dispersion of the gas, `n' is the number
density, and `R' and `M' are the radius and mass of the cloud.
These came to be known as `Larson's Laws.' Note that only two
of these relations are independent: if two of them hold then the third
must hold also.
The Model put forward here by Myers and Goodman is an equilibrium model
for molecular clouds. In it we have a uniform self-gravitating sphere,
surrounded by a medium of negligible kinetic and magnetic pressure.
It is in virial equilibrium. The key assumption, distinguishing this
from other models, is that they assume that the non-thermal component of
the kinetic energy is equal to the magnetic energy of the cloud.
It is the ``spherical, non-interacting cow model,'' where you assume
that the shape and environment of the cloud do not critically
determine the overall properties of the cloud; they only add scatter to
the data. This is usually a good first thing to do, and as you can
see from the data most of these assumptions seem to be justified (see figures
1 through 4, Paper II).
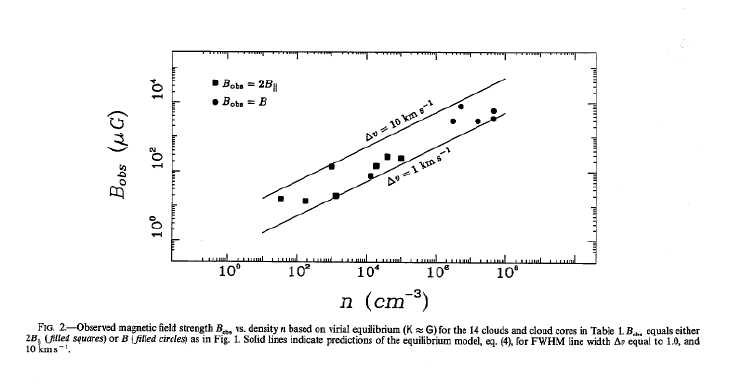
The magnetic field is a free parameter in this model; as you can see it does not appear in Larson's relations, and at the time data on magetic field strengths was hard to come by (see Paper I). So in fitting to the observed data, the model makes predictions for the magnetic field strenth that should be found on various size and density scales.
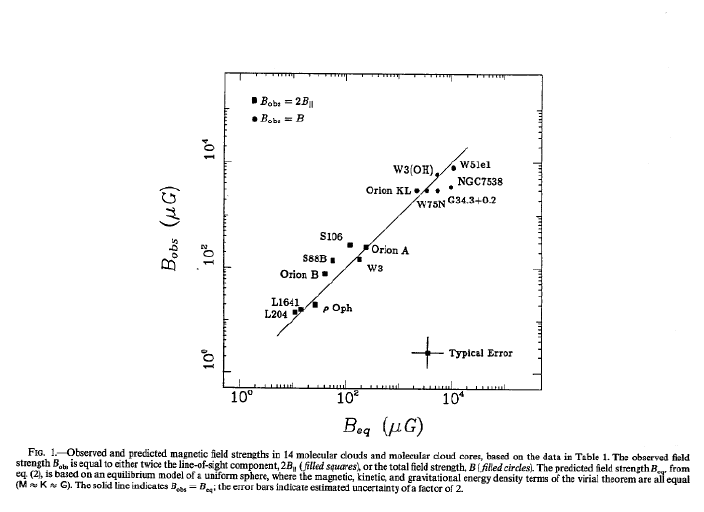
This is where paper I comes in. In this Letter, Myers and Goodman gather together all the data on magnetic field strengths in molecular clouds that they can find. They then keep all the data for objects which also have complementary observations of FWHM line width (\Delta v) and cloud size (R). They then use their equilibrium model to see what B-field strength it predicts, and compare this to the observed field strength. The very good agreement between model and observation is shown in fig.1 of the letter, reproduced below:

They also (in Paper II) compare their model to data for the Orion Molecular Cloud Complex. Their model predicts a field strength of B= 320 microGauss. This is much larger than the observed line of sight B=125 microGauss. This can be easily explained given that the line of sight B-field is on average a factor of 2 smaller than the true field, and by making the assumption that part (6%) of the non-thermal line width is due to something other than magnetic support.
The paper also has a lot to say about ambipolar diffusion. Their
model has the interesting feature of having a scale on which the timescale
for ambipolar diffusion is a minimum. This minimum is absent in most
other models. The minimum turns out to occur at the typical conditions
in low-mass dense cores. The minimum timescale is 2*10^{7} years
for these conditions with a 30 microGauss magnetic field. This is
a long time, given that a molecular cloud complex is not expected to live
much more than twice this long. Ambipolar diffusion was very trendy
at the time though, and was the only idea for why cores should collapse
so slowly (slower than the freefall time).
First of all, as we learned in class, molecular cloud substructures are definitely not spherical, and they are frequently not well defined in size at all. Secondly the density is something that is only determined up to a factor of ~2 from molecular line observations or extinction maps, and it is definitely not uniform -- the clouds are centrally condensed. Fig.4a,b in paper II shows that uncertainties in density and size are indeed the dominant uncertainties in the model. This large scatter is presumably due to clouds not having a well defined single radius, or a well defined single density. An alternative explanation is that the scatter is real and is due to clouds being out of virial equilibrium. If this were true, however, the assumption of virial equilibrium in fig.4b would not reduce the scatter as much as it does. This is strong evidence that the clouds are close to being in some sort of virial equilibrium.
It is noted that in fact the non-thermal support does not have to be magnetic: it just needs to have a pressure independent of cloud size in order to reproduce the observed scaling relations. See Fleck (1988, in the same journal volume) for an alternative view involving magnetic and non-magnetic turbulent support with external pressure.
It is argued in paper II that there is circumstantial evidence that
ambipolar diffusion (AD) is occuring in low mass cores. This is based
on the fact that the minimum timescale for AD is given for the conditions
corresponding to those in low mass cores i.e the fact that they are what
are observed indicates that this is the process governing the collapse
of cores. Recently, AD has gone a little out of favour, as compared
with dissapation of turbulence on small scales, however that happens (see
Evans below).
Quotes from Evans:
Summary of Isolated Star Formation
``Distinct cores can be identified in tracers of dense (n 104
cm-3) gas; these cores are frequently associated
with star formation. There is no clear evidence that they are magnetically
subcritical, and some kinematic
evidence suggests that the decay of turbulence, rather than ambipolar
diffusion, is the critical feature. An
empirical evolutionary sequence, based on the spectral appearance of
dust emission, and detailed
theoretical models are now being tested by observations. The spatial
distribution of dust emission is
providing important tests by probing n(r). Predictions of the evolution
of spectral lines during collapse are
available for the simplest theory, and observations of some sources
match predictions of theory quite well.
Evidence of collapse is now strong in a few cases, and surveys for
distinctive line profiles have revealed
many more possible cases.''
Summary of Clustered Star Formation
``The cloud mass distribution found for lower-mass objects continues
to massive clouds, but less is known
about the distribution for dense cores. Very massive cores clearly
exist, with sufficient mass () to
make the most massive clusters and associations. These cores are denser
and much more dynamic than
cores involved in isolated-star formation, with typical n ~ 106 cm-3
and line widths about 4-5 times larger
than predicted from the line width-size relation. Pressures in massive
cores (both thermal and turbulent)
are substantially higher than in lower-mass cores. The densities match
those needed to form the densest
clusters and the most massive stars by coalescence. There are some
cores with evidence of overall collapse,
but most do not show a clear pattern. There is some evidence that more
massive regions have flatter
density profiles and that fragmentation increases with mass, but more
studies are needed. High-resolution
studies of nearby regions of cluster formation are finding many clumps,
limiting the feeding zone of a
particular star-forming event to l ~ 6000 AU, much smaller than the
reservoirs available in the isolated
mode. In some cases, the clump mass distribution approaches the slope
of the IMF, suggesting that the
units of star formation have been identified. Studies of intermediate-mass
stars indicate that a transition to
clustered mode occurs at least by a spectral type of B7.''
A reading of relevant parts of Evans review shows that much of the picture
of star formation has not changed in terms of what Myers and Goodman propose.
Magnetic field measurements in molecular clouds are still very hard to
make and there are not many of them. See Crutcher
(1999) for recent measurements of Zeeman splitting in radio observations
which seem to support the Myers and Goodman hypothesis. He finds
that density is proportional to B squared, consistent with fig.2 of Myers
and Goodman (paper I), and consistent with their equilibrium model of paper
II. His plot is shown below, with the Myers and Goodman (paper I
fig.2) plot beside it for comparison:
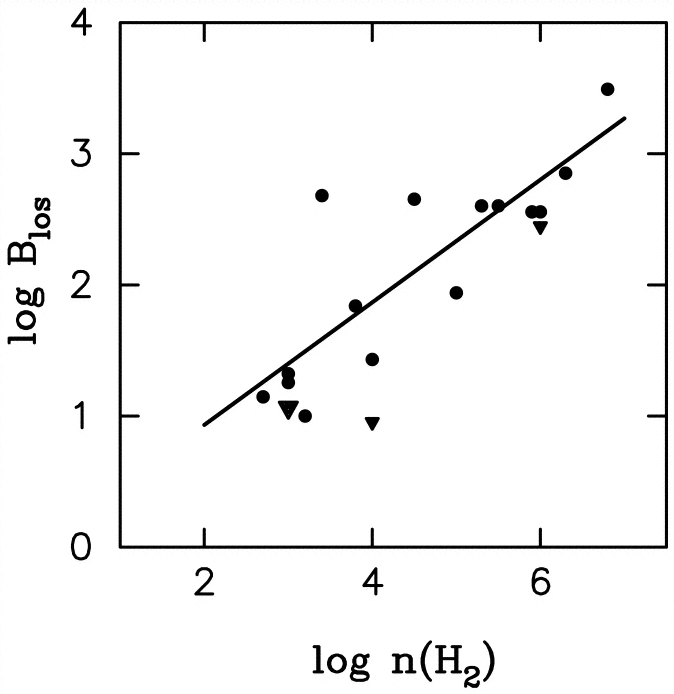
Crutcher (1999)
Myers and Goodman (1988)
Interestingly, Crutcher also considers uniform spherical clouds in his paper, indicating that analytic models have not grown significantly in complexity since 1988.
On the question of magnetic support, see Padoan
et al. (1999)
Quotation from the abstract:
``We compare the statistical properties of J = 1 0 13CO spectra
observed in the Perseus molecular cloud
with synthetic J = 1 0 13CO spectra, computed solving the non-LTE
radiative transfer problem for a
model cloud obtained as solutions of the three-dimensional magnetohydrodynamic
(MHD) equations. The
model cloud is a randomly forced super-Alfvénic and highly supersonic
turbulent isothermal flow.
...We present several statistical results that demonstrate remarkable
similarity between real data and the synthetic cloud. Statistical properties
of molecular clouds like Perseus are appropriately described by random
supersonic and super-Alfvénic MHD flows. Although the description
of gravity and stellar radiation are essential to understand the formation
of single protostars and the effects of star formation in the cloud dynamics,
the overall description of the cloud and of the initial conditions for
star formation can apparently be provided on intermediate scales without
accounting for gravity, stellar radiation, and a detailed modeling of stellar
outflows''.
These sorts of simulations are probably the only way of developing a
more realistic model of molecular clouds, where the cloud is not in any
sort of equilibrium, nor is it of uniform density or spherical. This
will hopefully bring new insights into the conditions in molecular clouds
and the processes leading to star formation.